Loss of surnames in small communities: a model
We recently visited my wife’s grandmother’s village of origin, on the eastern edge of the Massif Centrale in France. It is tiny and relatively remote, in good but very hilly farmland. The town has a population now of under 500, and was maybe twice that during her grandmother’s childhood. Visiting the graveyard it struck us that certain surnames came up again and again (Débatisse, Barge, Goutorbe, Pras, Copperé, Fragne). Naturally in small communities (particularly before easy transport) people will marry locally, but to contemporary eyes it seems almost incestuous: everyone seems related to everyone! But if a surname is common, it is relatively likely for spouses to have the same one, without being particularly closely related.
This got me thinking about the effect of community size on the distribution of surnames. Without in-migration, or mutation of surnames, it is intuitive that the number of distinct surnames will fall over time, under the common rule that children will take their father’s surname, not their mothers.
I thought about modelling this. My first attempt uses some code I had lying around for running Wright-Fisher population inheritance models. WF models work with a fixed population where each generation reproduces once; each individual matches with one random other. Thus each individual procreates on average twice and at least once, population size is fixed and generations do not overlap. Normally FW models are used to think about population genetics, and imitate biology with a “crossover” rule where each child inherits genetic material from both parents, approximately half from each. For this model we can replace the crossover rule with a very simple one: your name is 100% your father’s and 0% your mother’s. It’s a very restricted model, but its simplicity makes it easy to work with.
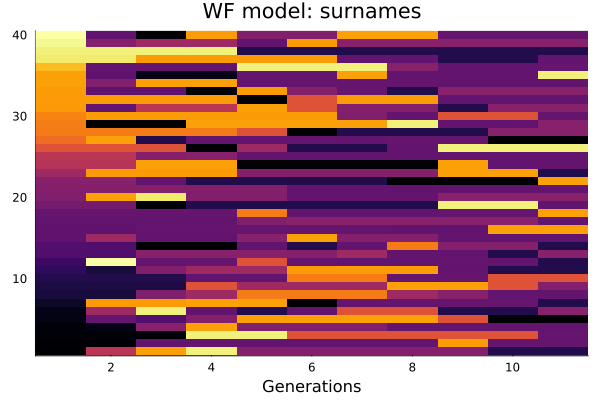
We start with 40 individuals, half male, half female at random. Everyone has a different surname at time 1, and gender of offspring is random. After 10 iterations there are about 8 distinct surnames (outcomes vary a lot from run to run).
We can represent the history of the model as a matrix (shown here a heatmap). Each column represents a generation, and each colour a surname. The cell to the left is always one of the two parents (the other parent is random).
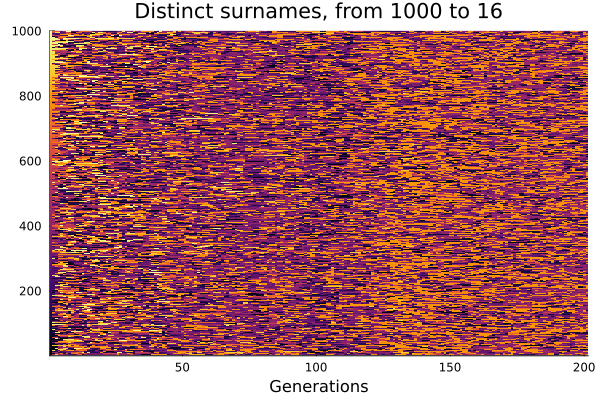
What about larger numbers for a longer time? Here plot the progress from time 1 to time 1+200, for a population of 1,000.
It’s perhaps clearer to summarise the number of unique surnames at each generation. Because there is an important element of randomness in the process, we run it 100 times, to see how consistent the process is. The pattern seems exponential (constant rate of decline) at first glance, but in fact the rate of decline is higher initially and declines. Notably the randomness is far less consequential than the big initial dip.
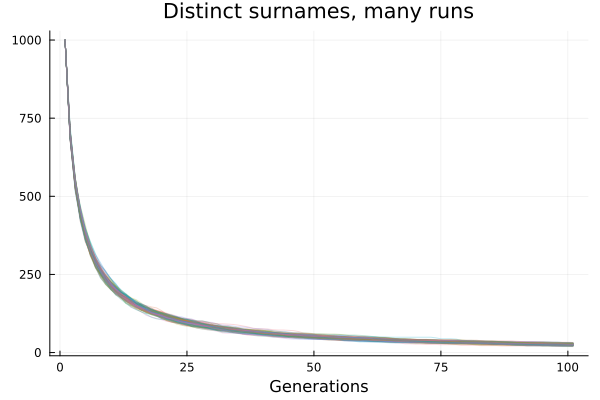
The rate of decline is consistent with a Power Law relationship, rather than an exponential one, i.e.
\[ y = ax^b \]
with \[ b \approx -0.8 \].
Begining at time zero gives a huge immediate drop from one surname per person, but let’s look instead at the generations 25 to 50. This starts us at a lower level, perhaps more realistically, and shows a more gentle drop:
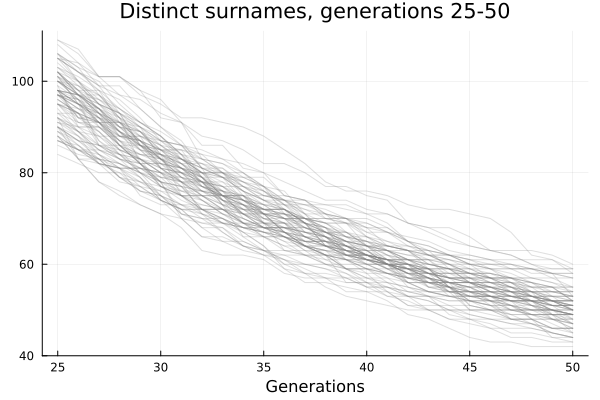
At generation 25, there are about 100 surnames in the population, and then 25 generations later (well, 750 years is a bit long…) we’re down to about 50 surnames. The more names there are, the rarer they are, and the faster they disappear, so we get a pattern of (more than) exponential decline. Which is to say, a very slow decline when the levels are low, but one that continues forever.
This is a very simple model, and misses out two major ways in which the number of surnames might increase: mutation and immigration. Mutation occurs in real life when names are qualified to distinguish branches (e.g., the Healy-Raes) or may change accidentally (e.g., Singleton mistranscribed as Fingleton). Immigration is simply the in-migration of outsiders with new names: this might be rare in an isolated village, but will occur in real-life. In this cemetery, for instance, there is a big family tomb with the surname Patchoukine, hardly typical to the region. The oldest people buried in it are two men (likely brothers), born in 1939 and 1940, with typical French forenames. One can guess that they were children of refugees, from Poland, the Baltic or even Russia, called Pachukin or perhaps Пачукин.
Postscript
There is a long history of work on surnames going extinct, at least as far back as Galton. Wikipedia’s page on the Galton-Watson process is very informative.